4 Minute Read
I regularly take the train to work. One thing I’ve noticed is how people instinctively seek out double seats to claim as their own. They’ll walk down the carriage, looking for that extra space to spread out and avoid interacting with anyone else.
Molecules come in all shapes and sizes, and understanding these shapes is key to predicting how they interact with one another. VSEPR theory, or Valence Shell Electron Pair Repulsion theory, can help us predict the shapes of molecules based on the principle that electron pairs repel each other. They try to stay as far apart as possible, much like passengers on a train who hope to avoid sharing a seat.
The main factor that determines the shape of a molecule is the repulsion of electrons. We find electrons in two places: bonds and lone pairs. The shape of a molecule will be arranged such that these regions of electron density (bonds or lone pairs) are as far apart as possible.
The first step in determining a shape is counting the number of regions of electron density. It often helps to draw a dot and cross diagram for this.
Let’s take carbon dioxide (CO2) as an example:
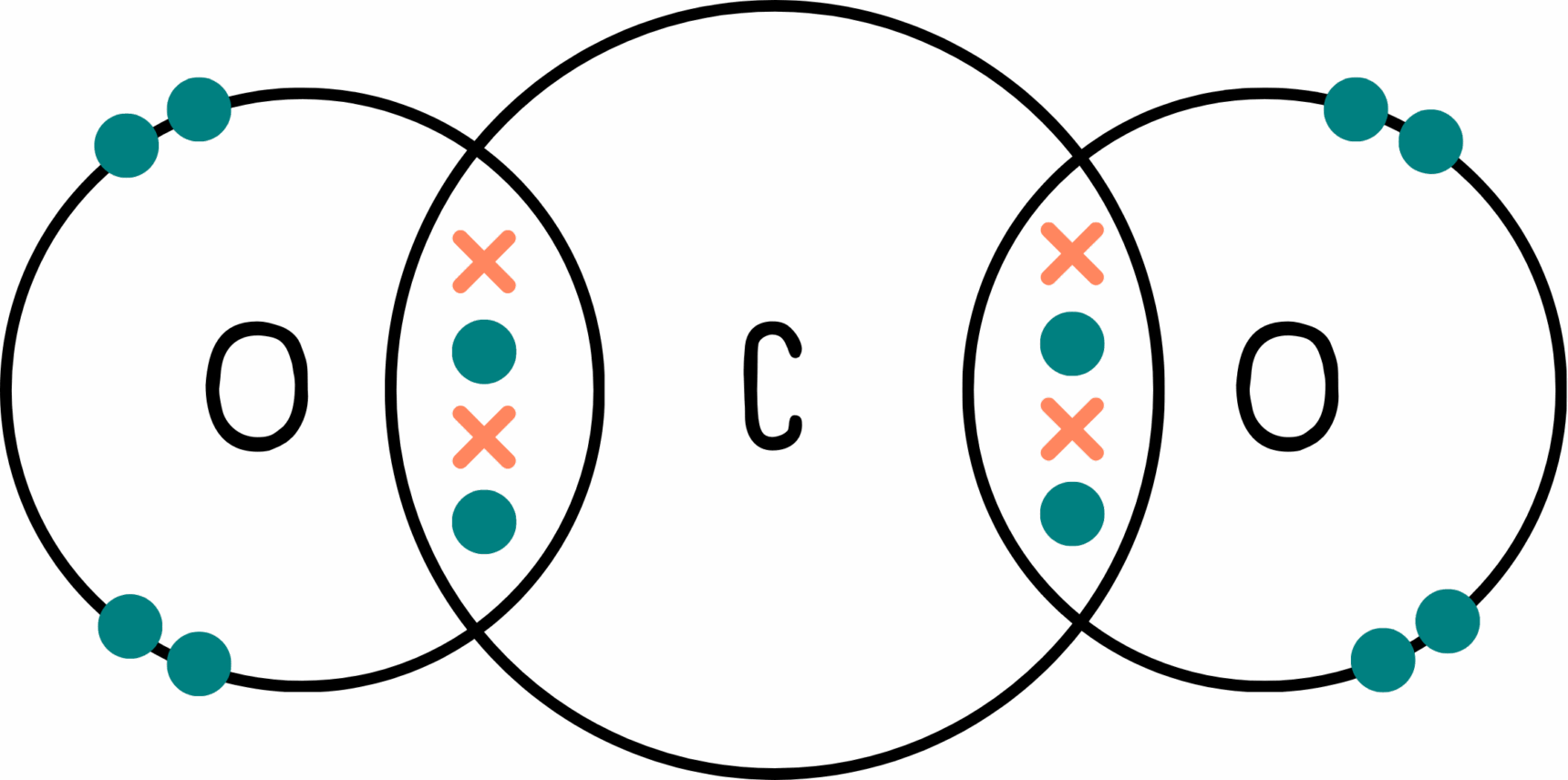
Carbon is the central atom. We can see that the carbon atom has two double bonds and no lone pairs.*
The two regions of electron density repel as far apart as possible, so in this case, we end up with a linear molecule, where the bond angle is 180°:
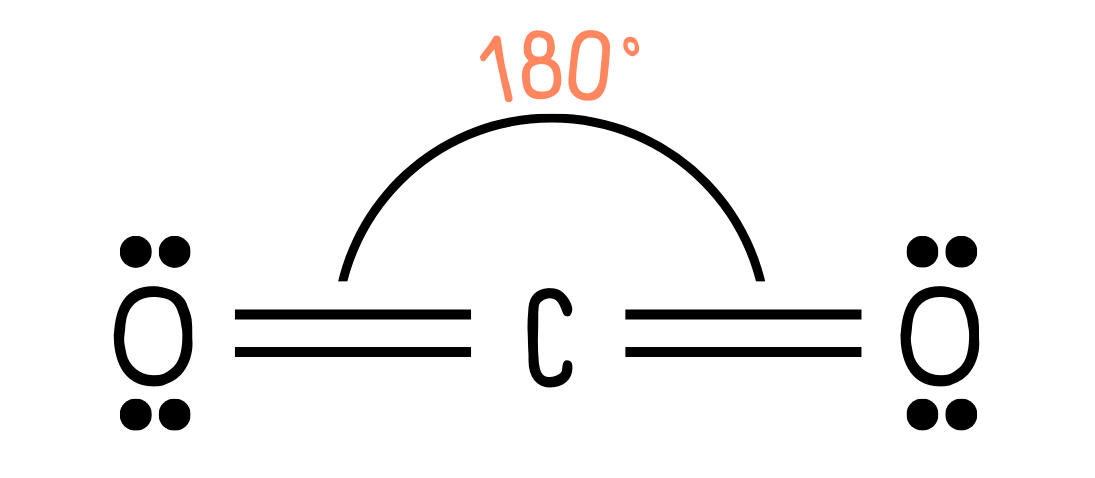
*Note that in A Level Chemistry, a double bond is treated the same as a single bond. However, in reality, double bonds exert greater repulsion than single bonds.
Know the basic shapes!
In order to answer questions on VSEPR theory in A Level Chemistry, you have to learn the basic shapes that can be formed from different numbers of bonds. This is summarised in the table below.
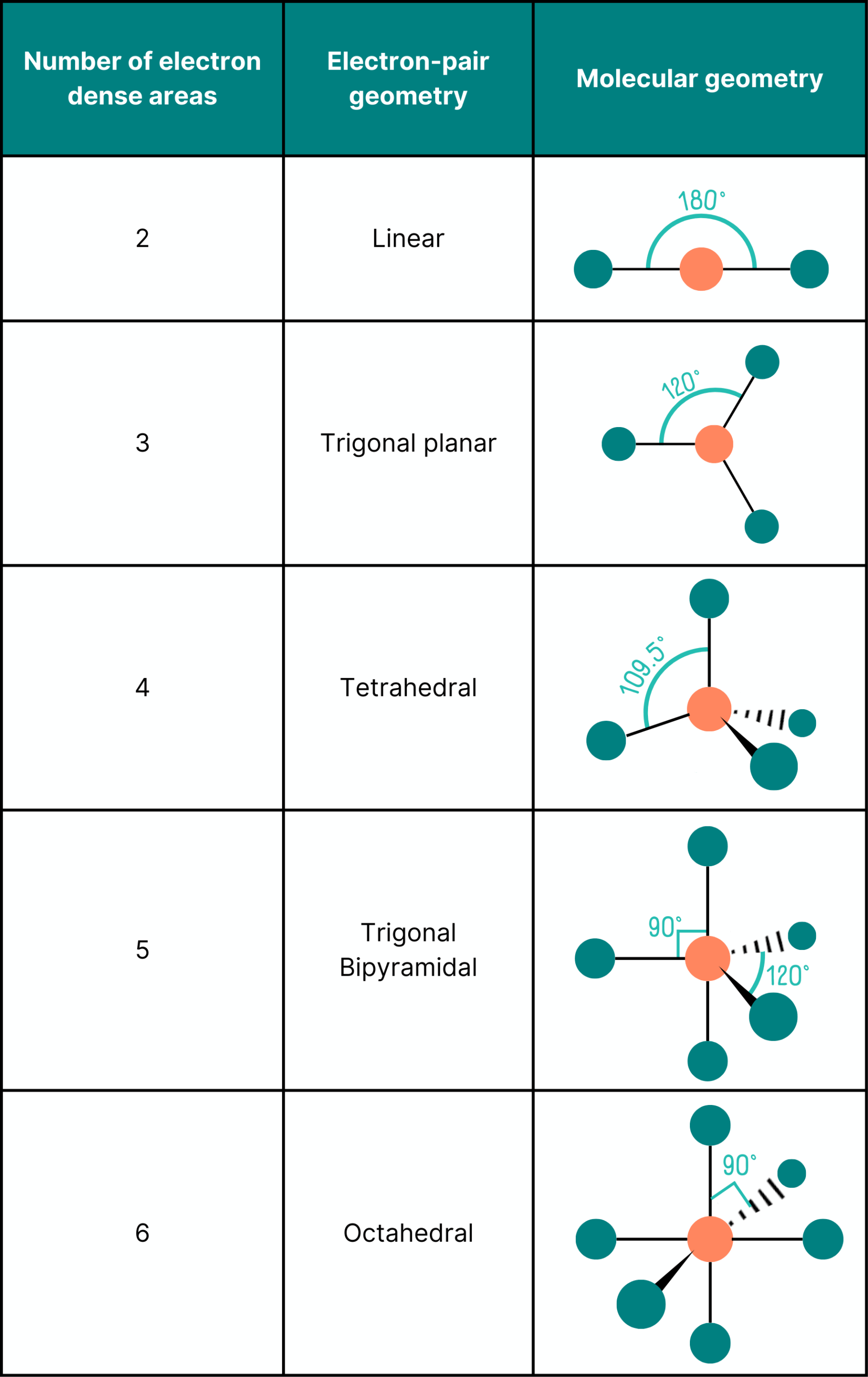
Most A Level Chemistry exam boards expect you to know the shapes formed from two to six regions of electron density, but check your exam specification!
Let’s look at another example, SF6. First we draw a dot and cross diagram:
Now, we count the areas of electron density around the central atom, S. The sulfur atom has six bonds. If we have memorised the table above, we know that for all bonds to be as far apart as possible, they will adopt an octahedral arrangement with an angle of 90°, as shown below:
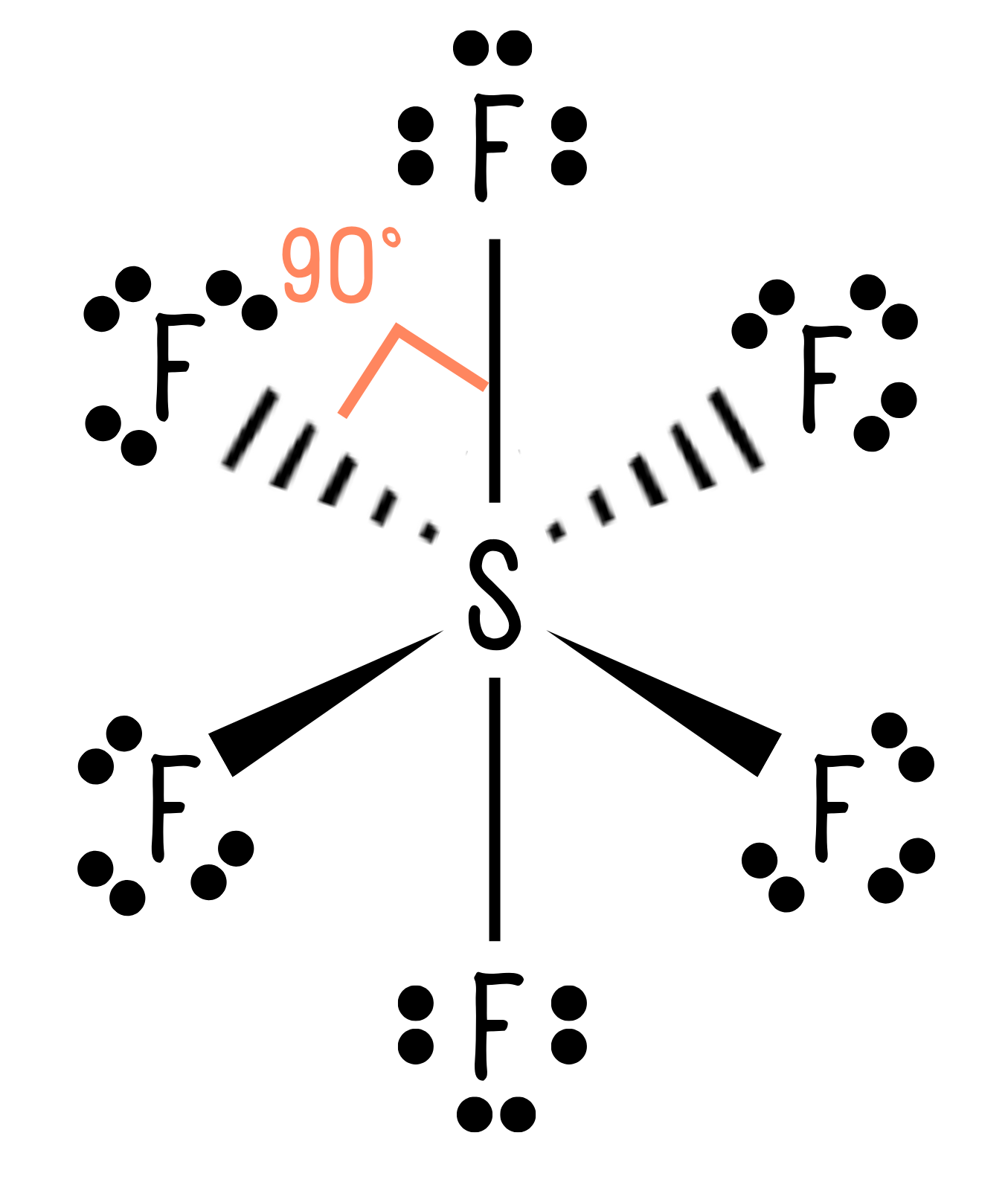
So far, so good. But what happens when we add lone pairs into the mix?
VSEPR theory and lone pairs
We’ll take ammonia (NH3) as an example. The dot and cross diagram for ammonia is shown below.
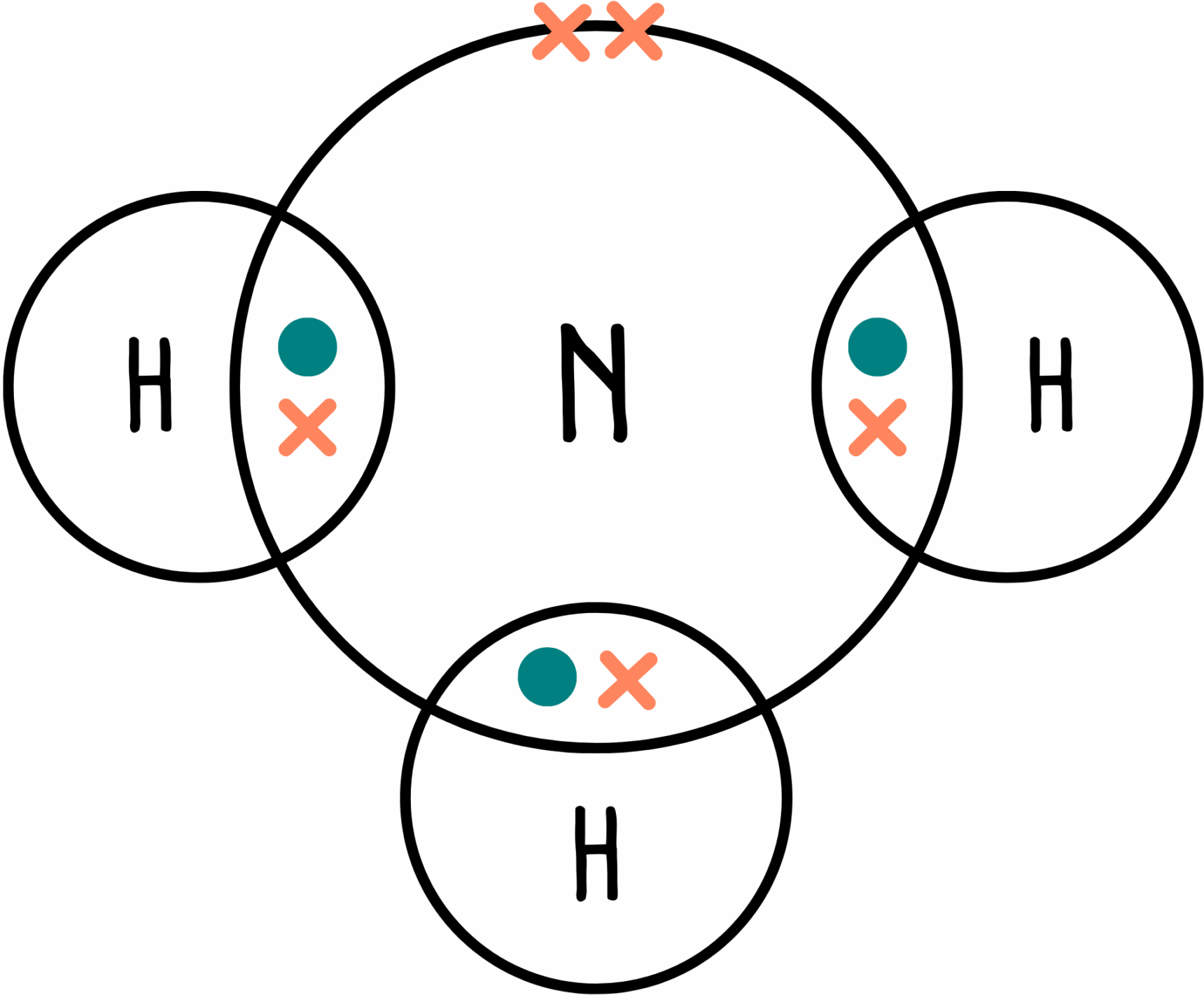
Let’s count the number of regions of electron density around the central nitrogen atom. We have three bonding pairs plus one lone pair, giving us a total of four regions of electron density. Looking at our table, we would expect a tetrahedral molecular shape.
The problem is, there are only three atoms, so we end up with a tetrahedral shape with one atom missing. This molecular shape is no longer tetrahedral. Instead, we refer to it as trigonal pyramidal.
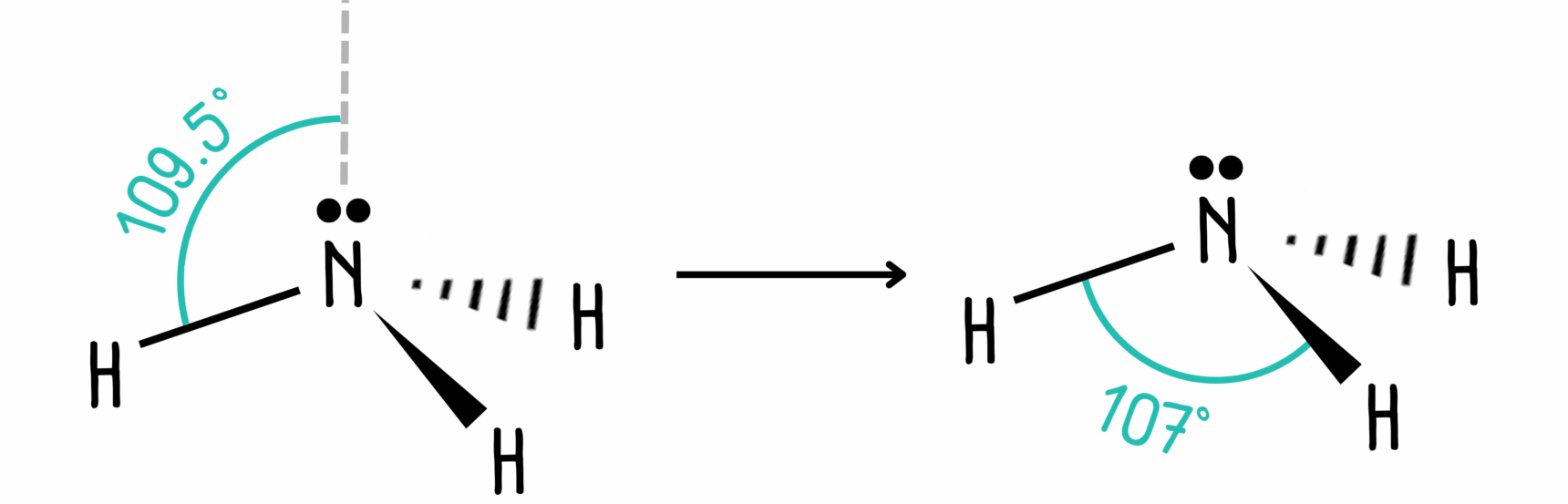
The bond angle is slightly different from what we would expect. Lone pairs repel more than bonding pairs because they are closer to the central atom. As a result, the bond angle is slightly smaller (by about 2.5°) than it would be in a tetrahedral molecule. In fact, it is 107°.
Let’s look at water (H2O).
The dot and cross diagram shows two bonding pairs and two lone pairs:
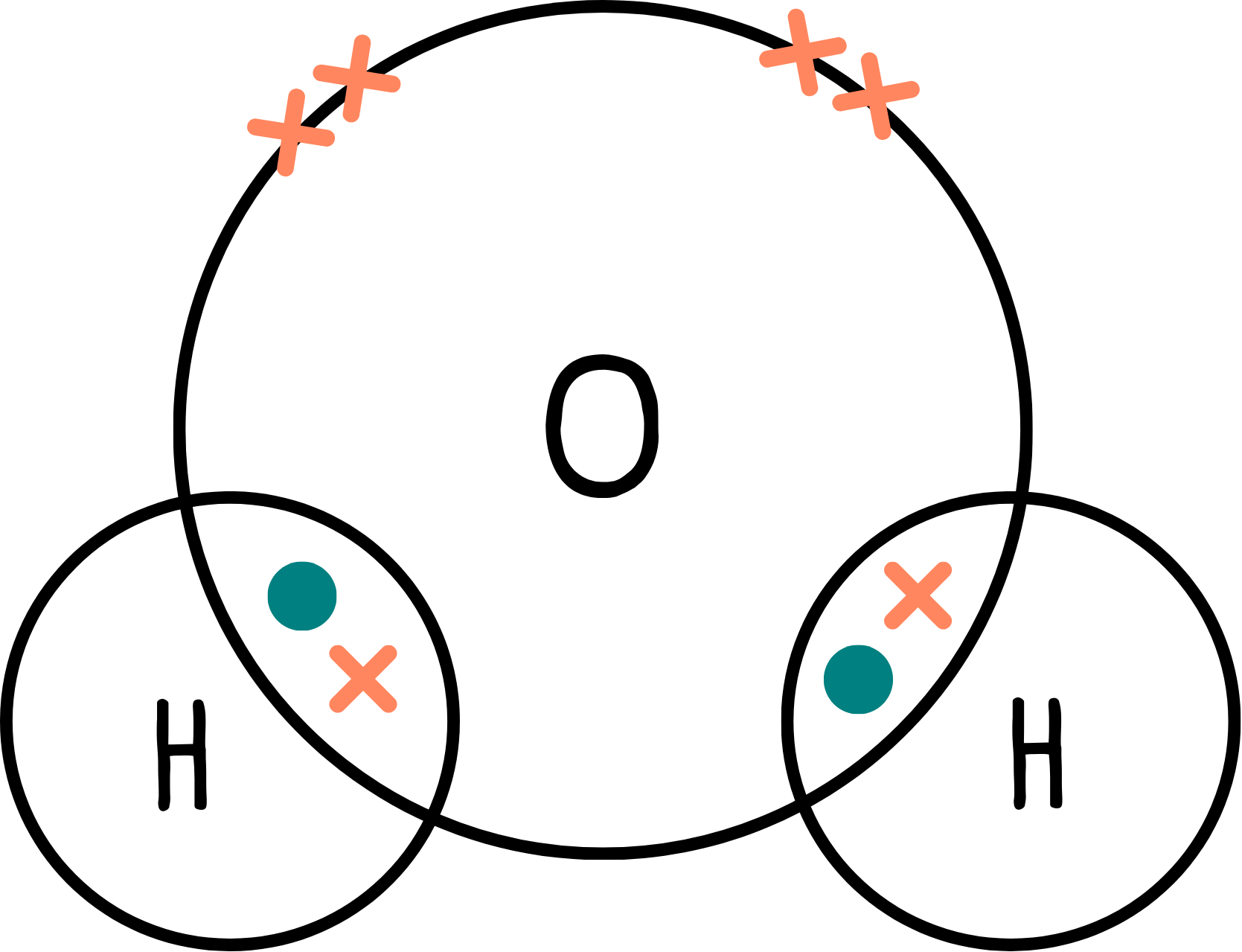
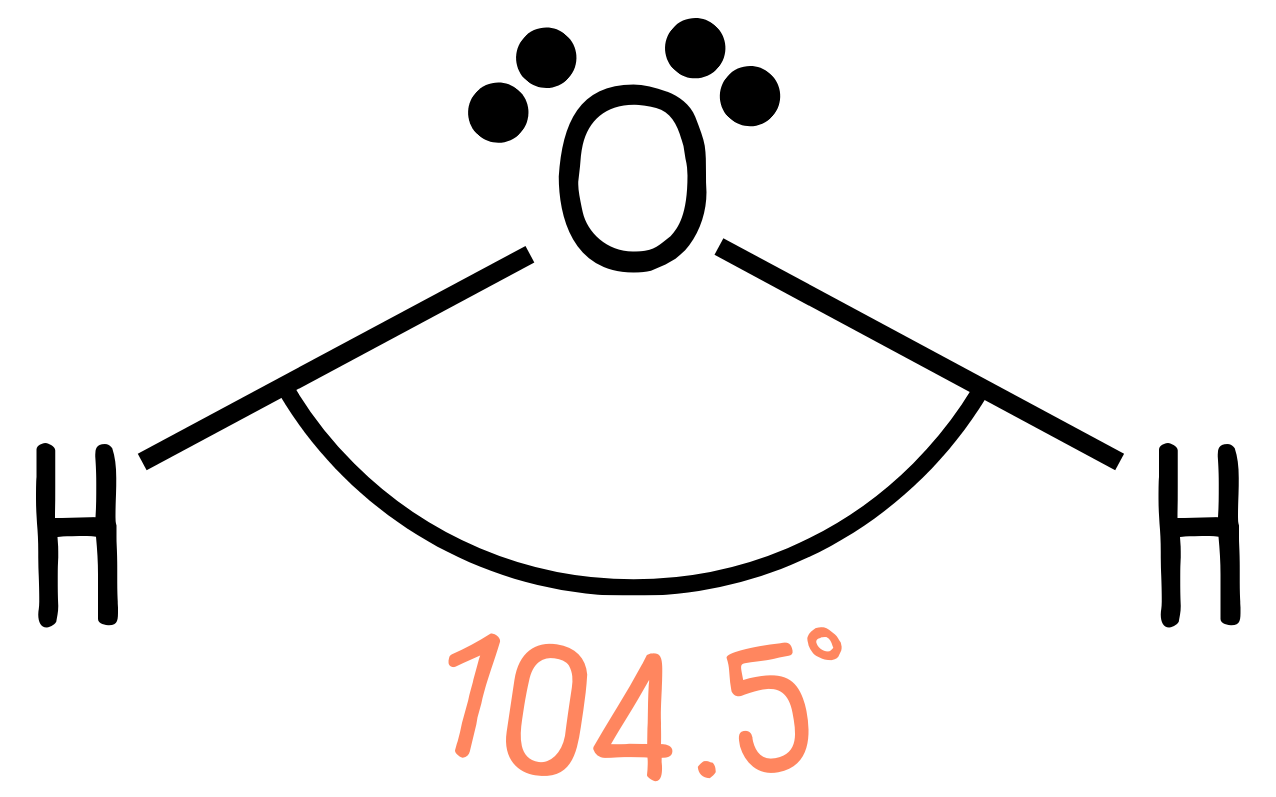
We have four regions of electron density, but this time we have two lone pairs, so we would expect the bond angle to be even smaller than 107°—and in fact it is 104.5°.
Once you add lone pairs into the mix, the table of shapes becomes a little larger.
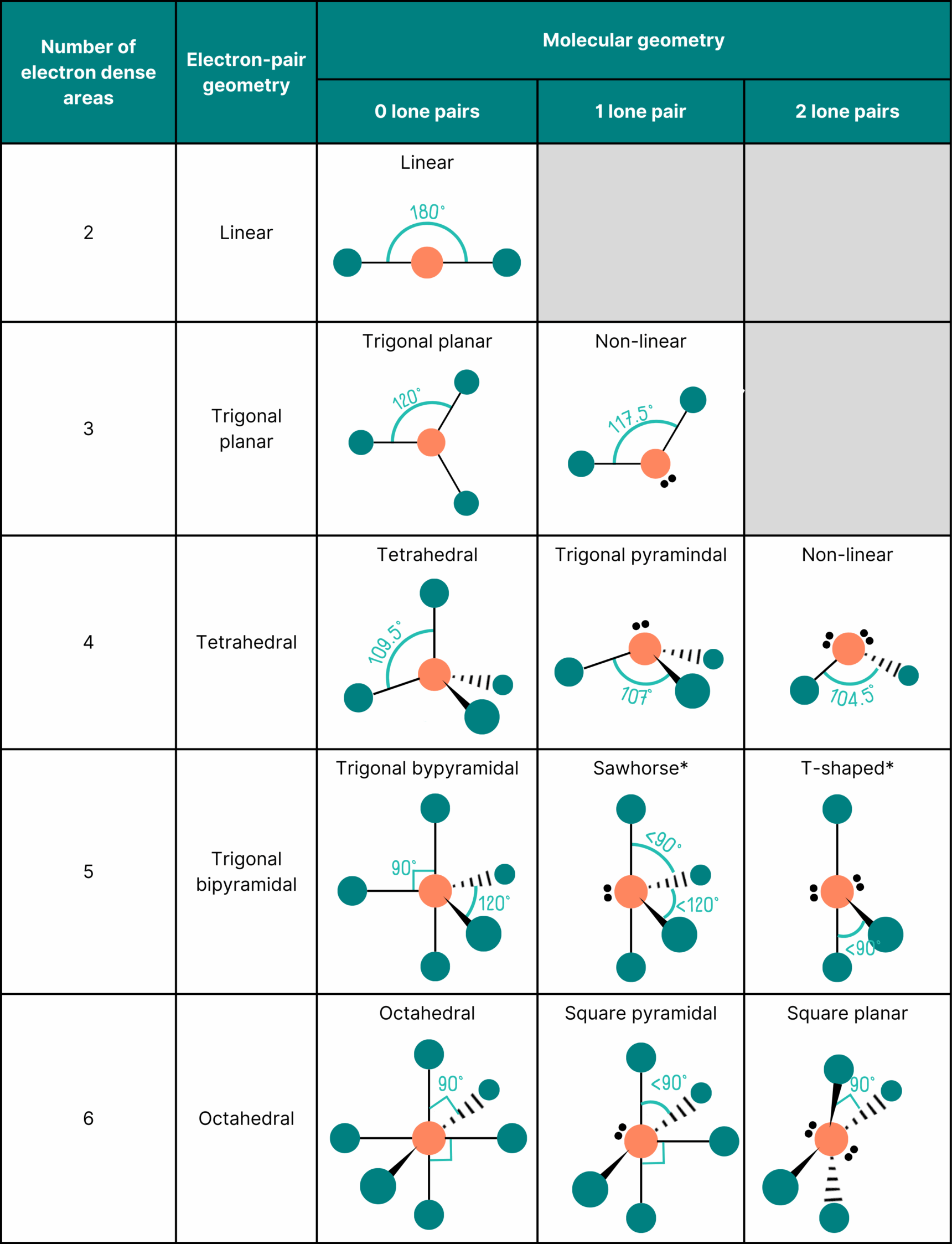
*Note that you won’t be expected to recall the name or bond angle of molecules with sawhorse or T-shaped geometries.
The key takeaway is that you need to learn the table above. Once you’ve done this, it’s a matter of following a couple of simple steps to figure out the shape. And next time you’re on a train searching for a seat, I wonder if you’ll think of VSEPR theory?
Struggling with other aspects of organic chemistry? Check out our student blog articles on getting to grips with skeletal formula, drawing reaction mechanisms, and making sense of NMR spectroscopy.
Copy URL
Comments