Tackling explanation questions in A Level Physics

A Level Physics explanation questions generally fall into one of three categories: recall, application, and practical questions. In this article, we will focus on how to tackle some of the harder types of application questions for which we will do some full examples. Before this, let’s briefly discuss the other two question types.

Recall questions

Recall questions are found in the early parts of a question and rely on you remembering the answer or being able to describe a process. Examples include:

• State Hooke’s law
• Describe the formation of a stationary wave
• Explain how the photoelectric effect provides evidence for wave-particle duality

These questions don’t require the introductory context that may have been provided for the rest of the question.

To prepare for recall questions, I’d suggest finding similar past exam questions and comparing their mark schemes. The common phrasing across the mark schemes demonstrates the wording and scientific language typically required to gain full marks. By comparing the phrasing seen in past questions, you can also learn to recognise the patterns in how questions are posed. These patterns can be quite predictable, so with a little detective work and memorisation, you can do well on these types of questions.

Practical questions

Practical questions tend to start with the words ‘explain how’, ‘describe how’, or ‘outline a procedure that’. These need to be answered by stating how the practical should be conducted to provide precise and accurate results, or how data already taken should be analysed.

When outlining a practical procedure, you should state what measurements need to be taken and with what equipment. In addition, you should add any particulars to make sure the measurements will be precise. For example, to determine the diameter of a wire, you should state that you need to ‘measure the diameter with a micrometer three times at different points along the wire’, or when making length measurements, you may need to mention the use of a set-square to ensure things are perpendicular or parallel. Providing the interval of the independent variable over which to make measurements is often also needed.

When responding to data analysis questions, you should focus your answer on describing what graph to plot and what the gradient represents. If a table is provided, you may first need to describe any additional data manipulation that must be done before you can sketch the graph. Since the gradient will have meaning, you should always aim for a straight line graph. This may require a little mathematical manipulation of the formula that relates the quantities. You should state that you intend to determine the gradient of the graph and then also what the gradient is equal to. Then, conclude by linking this to the quantity you are trying to determine.

Application questions

Application questions are usually found towards the end of a question and often involve a change in the situation at hand. Alternatively, they may require you to justify a claim. To better understand how to approach these types of questions, we will discuss two examples.

Example 1

Let’s say we are given the circuit in Figure 1 below that showcases a potential divider with a thermistor in it. The exam question asks what happens to the potential difference V_t across the thermistor as only its temperature increases. Give yourself a minute to think about the answer. This type of question is typically worth 3 to 4 marks.

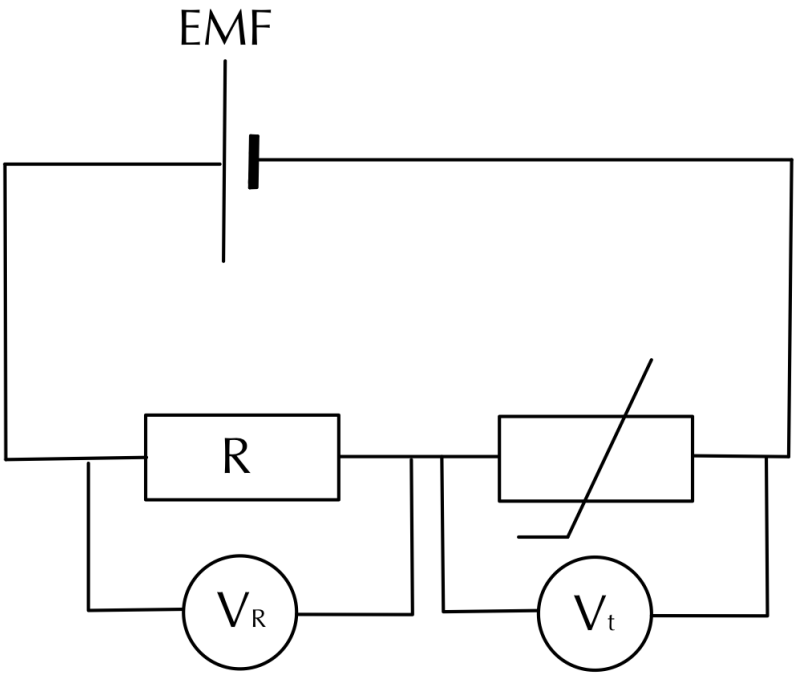
Figure 1: A potential divider circuit where the thermistor offers a variable resistance as temperature changes.

Did you automatically try to say that it would increase, decrease, or remain constant? Throughout my teaching and tutoring career, the biggest problem I see with students trying to tackle these explanation-style questions is their expectation to know the final answer immediately rather than puzzling it out from the information provided.

Instead, we should focus on the change that has occurred, as it often leads to a small fact that can provide the starting point for solving the puzzle (and often, the first mark). In this example, the change is that the temperature of the thermistor will increase. Your first marking point is to write down that if the temperature of the thermistor increases, then its resistance R_t will decrease. This is a key fact you need to remember, and every topic will have a few such facts that provide the starting point for solving various problems.

After stating this fact, it is then your job to figure out what the consequence of this decrease in resistance is. Now, you may be tempted to instantly try to use V_t = IR_t and state that as R_t decreases, V_t decreases. However, this does not seem enough for a 4-mark explanation question, so we are most certainly missing something! This type of thinking has incorrectly assumed that the current remains constant when, in fact, it will change.

To correctly puzzle it out, we should follow the trail of small facts and their consequences. Hence, how does a decrease in the resistance of the thermistor affect the circuit? If you’re thinking that it will decrease the total resistance R_TOT in the circuit then you’d be correct! This has a knock-on effect on the total current I in the circuit as I = EMF/R_TOT. Thus, as the total resistance decreases, the current in the circuit increases.

Now, at this point, you may be tempted to think that we can surely use V_t = IR_t. However, since both the current through the thermistor and its resistance have changed, we have no idea as to what the final change will be for the potential difference across it.

The only way we can work this out is to look at how the potential difference across the fixed resistor R will change. For this resistor, we can apply V_R = IR since R remains constant. As the current I increases in the circuit, we can see that the potential difference across the fixed resistor will also increase.

We are now almost at our final answer! By applying Kirchhoff’s second law, which for the loop in this circuit gives that the EMF = V_R + V_t, we can see that since the EMF is fixed and V_R increases, V_t across the thermistor must decrease. This gives us the same answer as before but is now correctly reasoned and will give us all the marks.

In this example, we can see that we are always considering a small direct consequence that has occurred due to a change. In summary:

Change	Consequence
The increase in the temperature of the thermistor	Decreases the resistance of the thermistor
Decrease in the resistance of the thermistor	Decreases the total resistance of the circuit
Decrease in the total resistance of the circuit	Increases the total current of the circuit
Increase in the total current of the circuit	Increases the P.D. across the fixed resistor
Increase in the P.D. across the fixed resistor	Decreases the P.D. across the thermistor

In Figure 2 below, you will find two other questions that require the same application of ideas. You will find the answers at the end of this article but try to give them a go yourself first. Apply the following thinking:

1. How does the resistance of the component change?
2. How does this affect the total resistance in the circuit, and hence the current in the circuit?
3. How does the change in current affect the potential difference across the fixed resistor?
4. Using Kirchoff’s 2nd law, how does the potential difference across the component change?

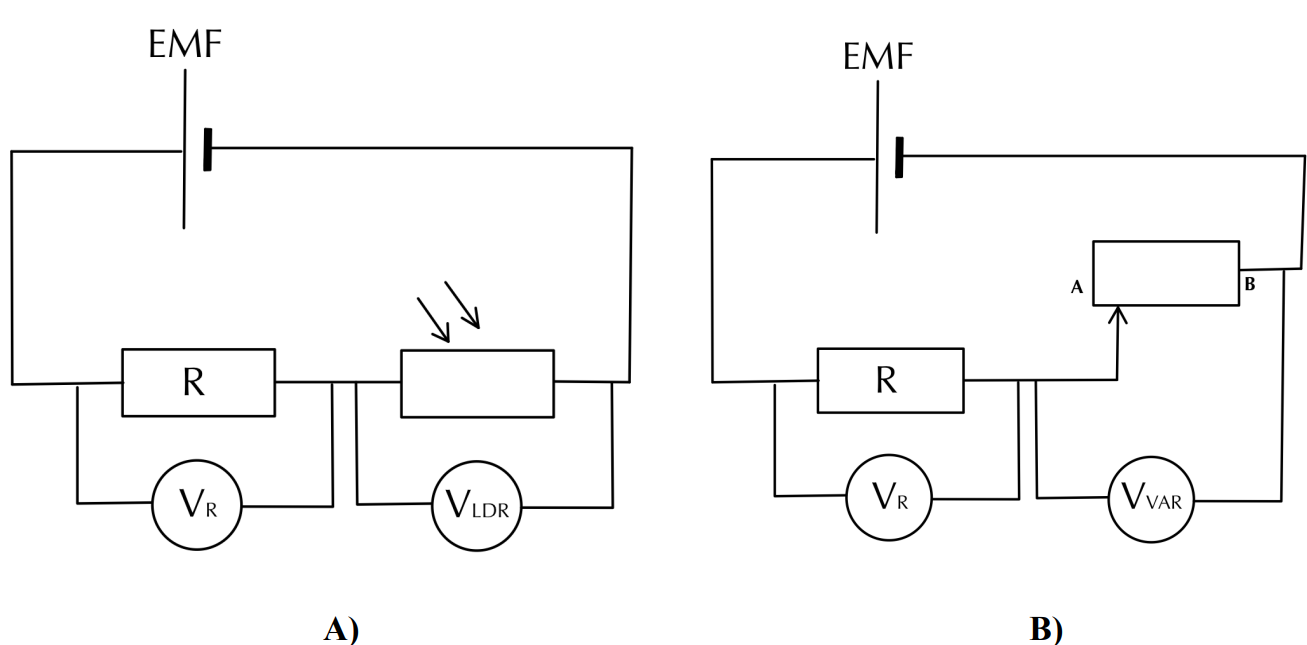
Figure 2: Answer the following questions: (A) If the intensity of light incident on the LDF decreases, explain how the V_LDR changes; (B) As the sliding contact moves from A to B for the variable resistor how does V_VAR change? Answers at the end of the article.

Example 2

Now, let’s look at another example from waves that is actually very similar in terms of our thinking process. We have a red laser pointing at a diffraction grating and observe the intensity pattern, as seen in Figure 3 below. The question tells us that the red laser is replaced with a blue one and asks how the diffraction pattern on the screen will change for 3 marks. Again, take a moment to think about this for yourself and see what you come up with.

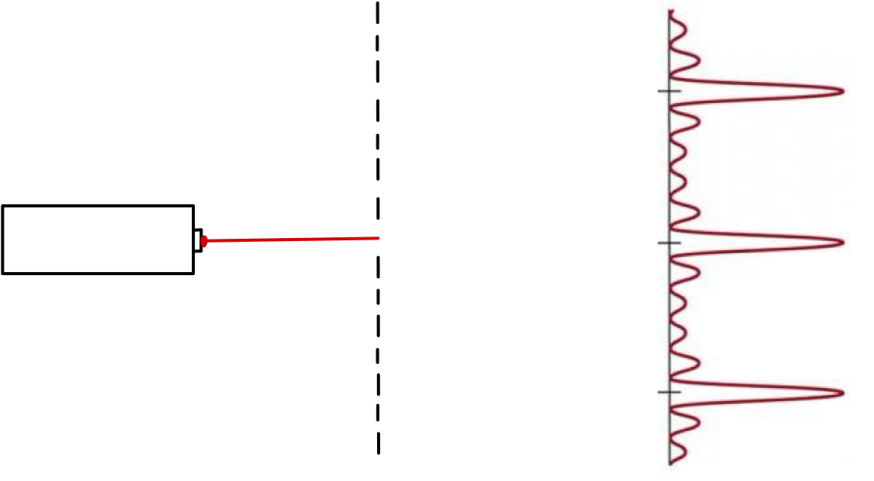
Figure 3: A red laser shines onto a diffraction grating causing an intensity pattern to be observed on a screen behind it.

You may be tempted to focus on the final answer first. Perhaps you’re thinking about whether you have more or fewer maxima, or whether the pattern widens or narrows. However, this approach often leads to a muddled response that may miss some of the marking points. Rather than reasoning backwards from an answer, consider the consequences of the change and then work things out step by step.

Hence, what does changing from a red to a blue laser mean in terms of physics facts? For this, you need to know the order of colours and how this relates to wavelength: R O Y G B I V, where red R has a longer wavelength than blue B. Simply writing down that the wavelength has decreased when changing from a red to a blue laser provides us with our first mark.

Now that we know that the wavelength decreases for blue light, we can consider the consequence of this. I’ve heard some teachers state over the years that you must always tackle explanation questions in words only, but this isn’t correct. You are allowed to use equations in questions as well as mathematical symbols to explain answers. My favourite sentence structure to use for this is: Since [place equation here], if….. then…. (try to point out what remains constant in the equation as well).

We can apply this to our current question using the diffraction equation: Since nλ = dsin θ, if λ has decreased while n and d are constant, then sin θ also decreases. If sin θ decreases, then the angle between orders will also decrease (think of how a sine wave increases from 0 to 1 as the angle increases from 0° to 90°, and so the reverse is also true). A smaller angle between orders means you can see more orders on the screen, which is the first and main conclusion we can make about how the pattern on the screen may change. You could’ve written that less diffraction occurs for blue light than for red. However, this typically isn’t specific enough at A Level and would likely only give you one mark. The other conclusion that may be worth a mark is simply stating that the pattern will be blue instead of red!

Further questions to consider: C) How does the pattern on the screen, as seen in Figure 3, change when we replace the diffraction grating with a single slit?; D) How does the maximum order observed change when we increase the number of lines per mm on a diffraction grating?

In conclusion

For these types of explanation questions, the following thought process is required:

1. What has changed and what is the key physics fact from this change? Write this down as it’s worth a mark.
2. What is the consequence of this key fact? Think in small steps rather than immediately connecting it to the question being asked. Write this consequence down and enjoy another mark.
3. Draw on any equations to help you determine what other consequences will happen. Remember that only two things can change, and everything else in the equation must be constant.
4. Rinse and repeat this process until the link to what the question is asking is clear. Then, write a final concluding statement.

This process should help you answer any explanation questions where a clear change occurs. If you struggle with these questions, it’s possible that you’ve not cemented your fundamental knowledge enough yet or are unsure about the key facts for each topic. If these are not at your fingertips, then, of course, these questions become impossible to gain full marks on. This is something that an experienced tutor can help you with, and is something I work with students on.

Happy problem solving!

---

Answers to questions in the text

1. When the brightness decreases, the resistance of the LDR increases. This increases the total resistance of the circuit, and as the EMF is constant and EMF = I_TR_T, the total current decreases. Since V_R = I_TR and R is constant for the fixed resistor, V_R will decrease. Given that EMF = V_R + V_LDR, this means that V_LDR will increase.
2. As the sliding contact moves from A to B, the resistance of the variable resistor decreases from a maximum to zero. Thus, the total resistance decreases in the circuit and its current increases. Since EMF = V_R + V_VAR and V_R = I_TR, this causes the potential difference across the fixed resistor to increase until it is equal to the EMF when the sliding contact reaches B. Thus, the potential difference across the variable resistor decreases from a maximum to zero as its resistance goes from a max to zero.
3. For this question, the key fact to recall is that the central maximum is always twice as wide as subsequent maxima in single slit diffraction, whereas in gratings, all maxima have equal widths. For a single slit, the central maximum has the greatest intensity, and that of subsequent fringes decreases significantly. In comparison, a grating has reasonably similar intensities across the fringes, only slightly decreasing outwards from the central maximum. This question was not one that needs puzzling out as such, as it only relies on these key facts at A Level. The reasoning why is too mathematically complex at this level.
4. The maximum order observed can be found by using θ = 90 degrees and solving for n. Since n must be a whole number, be sure to round down to find the maximum order observed, as the subsequent order won’t be visible. When the number N of lines per mm on a grating increases, then the grating spacing d = 1×10^-3/N will decrease. Since nλ = dsin θ, and sin 90 = 1, n = d/λ. As λ is constant and d decreases, the maximum orders observed will also decrease.

• Copy URL
• Share Article